1.3 Using this guide
This guide is available as part of the Myron distribution and can be viewed using Myron's book reader. It is also available in online and print formats. This section explains the type-setting conventions and terms used throughout the rest of the guide. It also explains how to use the navigation features of the book reader.
Because Myron runs on both Android and desktop systems, there are
occasional differences in the user interface. These are indicated in
the guide using the icons for Android ( ),
desktop (
),
desktop ( ) and windows tablet (
) and windows tablet ( )
to indicate when the text refers to a specific device.
In addition, the icon
)
to indicate when the text refers to a specific device.
In addition, the icon  is used
to distinguish comments specific to the online version of the guide
and
is used
to distinguish comments specific to the online version of the guide
and  is used for the print version.
is used for the print version.
Myron runs under one of two feature sets, generally referred to a lite and pro.
The guide indicates pro-only transformations and commands using the icon
 .
.
1.3.1 Navigation
If displayed using Myron's


 The book-reader provides navigation directly to the home page, the
table of contents, the index or the glossary. The menu is made visible
by touching the
The book-reader provides navigation directly to the home page, the
table of contents, the index or the glossary. The menu is made visible
by touching the
 icon at the top right of the book reader (or by touching the hardware
menu item on Android devices with small displays). Back and fore
controls
icon at the top right of the book reader (or by touching the hardware
menu item on Android devices with small displays). Back and fore
controls

 provide browser-like navigation through recently read pages. Content
controls
provide browser-like navigation through recently read pages. Content
controls


 mimic the navigation phrases.
mimic the navigation phrases.
 In the Android version of Myron, the table of
contents can also be seen by touching the
In the Android version of Myron, the table of
contents can also be seen by touching the
![]() icon at the top left of the book reader. Touching an item in the table
of contents displays that item in the reader. Touching the icon a
second time, while the contents are displayed, navigates back to the
algebra workspace.
icon at the top left of the book reader. Touching an item in the table
of contents displays that item in the reader. Touching the icon a
second time, while the contents are displayed, navigates back to the
algebra workspace.
When transformations are described in the guide, an imperative verb in a button-like frame indicates both the control and the action, like this: “select the divisor, then Distribute and Simplify ”. Such verbs are linked to their descriptions elsewhere in the guide, providing another axis of navigation.
1.3.2 Input and Display Representations
Embedded within the text, mathematical
expressions are displayed in one of two representations called the
The
The
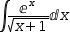


 All expressions in display form respond to being touched in the
book reader. When touched, the reader reveals the input form of the expression
and provides an option to copy it into Myron's workspace (after bookmarking the current location).
You can return to the bookmarked location in the guide by touching the
All expressions in display form respond to being touched in the
book reader. When touched, the reader reveals the input form of the expression
and provides an option to copy it into Myron's workspace (after bookmarking the current location).
You can return to the bookmarked location in the guide by touching the
 In the online version of this guide, expressions in display form are annotated
with the syntactic form of the expression. To see the syntactic form, click the mouse
on the display form.
In the online version of this guide, expressions in display form are annotated
with the syntactic form of the expression. To see the syntactic form, click the mouse
on the display form.
1.3.3 Terminology
When the term
Operands of binary operators are often identified by words constructed from the operator name and one of the suffixes -and or -end. For example, the add operator is applied to operands called addends (or summands) and the multiply operator is applied to multiplicands. Sometimes, the right operand is distinguished by the suffix -or. For example the divide operator operates on a dividend and a divisor; an integral specifies an integrand and an integrator. The use of explicit names adds precision to the text and often reduces the number of words necessary to convey a concept.
1.3.4 Annotations
In the book reader and online, the presence of a notation[1] is indicated by a footnote symbol and the notation itself is displayed in a popup when the highlighted text is touched. In the print version, notations are displayed as footnotes at the bottom of the page.